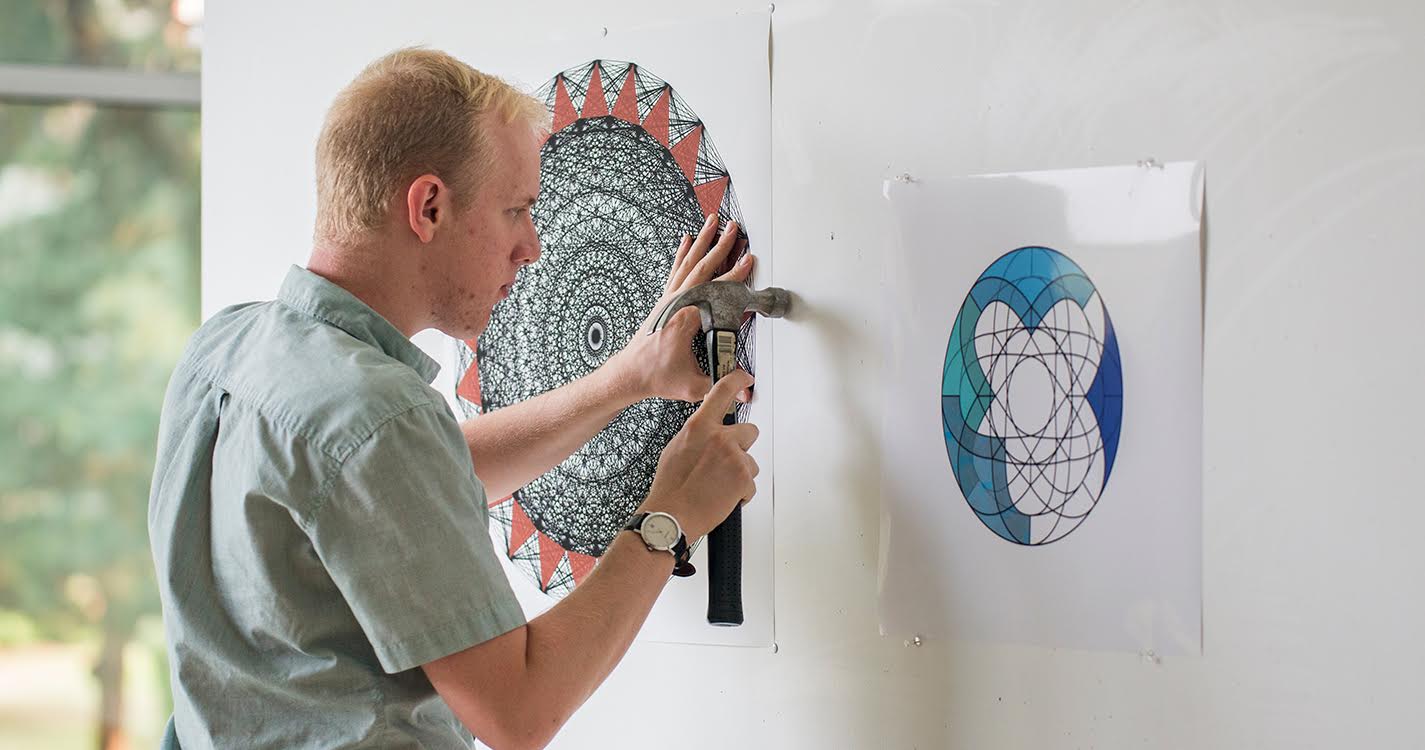
When you think about math-based art, a video of a Willamette professor lip-synching to The Jackson 5 might not be the first thing that comes to mind.
But students and faculty members recently challenged traditional assumptions about math and art — including their own — in a wide-ranging art exhibit featured in the Art Building Sept. 7-12.
Helmed by Associate Professor of Math Josh Laison and Assistant Professor of Art Cayla Skillin-Brauchle, the project tasked students with solving problems through both math research and the art process. Their work was supported through one of three interdisciplinary Liberal Arts Research Collaborative (LARC) grants awarded last summer.
The artwork
Arthur Stamey-Mills ’19, a studio art and film major, filmed faculty and students lip-synching to famous songs. He used arithmetic to warp footage during the editing process and set rules to distort each song’s speed. But his work also allowed the viewer to discover patterns in the overlapping images — similar to the way mathematicians might look for patterns in their research. To Laison, that feature best exemplified the exhibit’s title, “Creating Problems.”
Peri Hildum ’18, a studio art major, drew an array of pentagons across 16 sheets of paper to see how they behaved on a flat surface and created an algorithm to determine the color scheme.
Hildum says she’d “always struggled with math,” but felt more confident when she applied it to a medium she knew.
Two math majors — Allie Kerkhoff ’19 and Zech Hazel ’19 — found inspiration in graph theory, the study of the relationships between points and lines called vertices and edges.
Kerkhoff wanted to “give some meaning to abstract math,” so she created a map that represents the connection between several friends and cities. She also incorporated into the map the classic traveling salesman math problem of finding the fastest route between a set of points.
One of Hazel’s contributions was an intricate, digitally rendered complete graph — an elaborate Ferris wheel-like shape of circles and points connected by hundreds of lines. His goal, as well as Kerkhoff’s, was to find a new way to make graphs nonsymmetrical with the least number of “stamps” represented by different-colored shapes.
Comparing processes
Faculty members also created art, and along with students ran into expected differences between the fields in terms of outcomes.
“When mathematicians are writing a proof or theorem, there’s one way to do that,” Skillin-Brauchle says. “But in art, we have multiple ways to communicate the same idea.”
They also discovered some surprising similarities. Both fields provide rules or theories to help develop ideas for projects or proofs. Mathematicians and artists also take risks during their respective processes and accept failure as integral to the effort.
Students often think they’re not a math person because they didn’t understand it at first, but Laison notes that mathematicians, just like artists, keep trying.
In addition to being a great learning experience, the final art exhibit provided an opportunity for the public to see math in a different light.
Laison says, “You could walk through the mathematical ideas in a way that I’ve never done before. It was a living thing.”